[Free] Evaluate JavaScript Extension. Math expression. Source code

[Juan_Antonio]

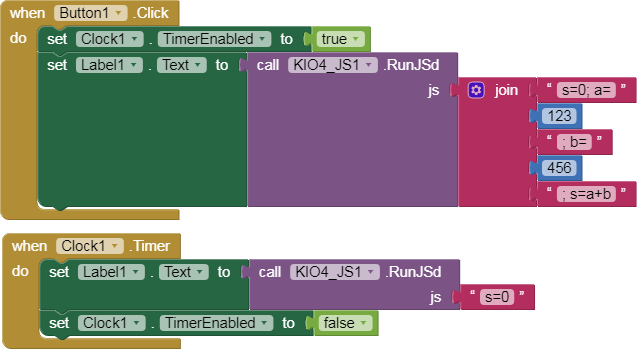
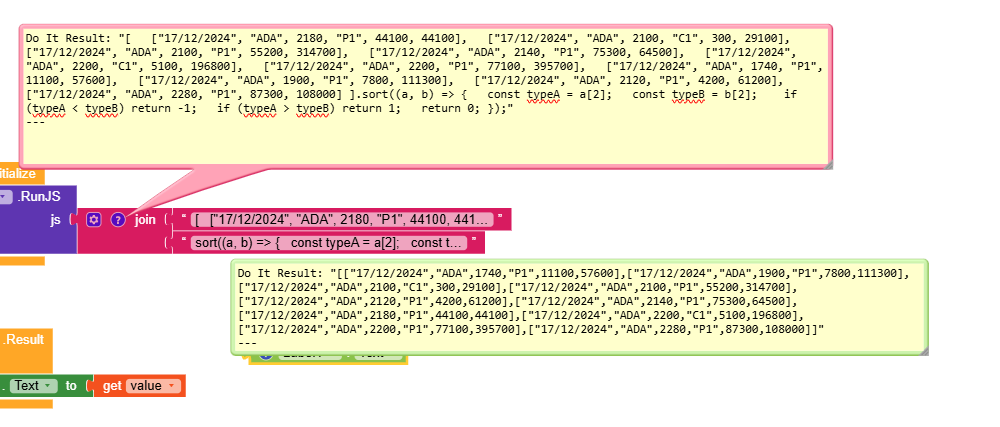
5.- Stress test this extension. Finding probability using the Normal Distribution.

p51f_runJs_Normal.aia (11.3 KB)

We are going to find the probability of a normal distribution using this extension. Comparison with block code.

We will follow this video:
https://www.youtube.com/watch?v=Rionve04Dvs

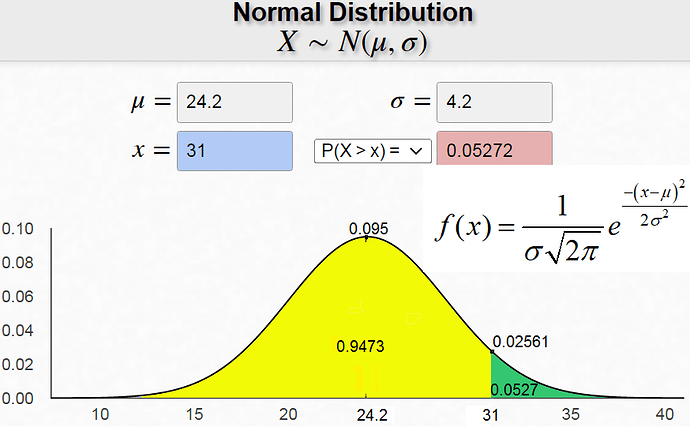
Scores are normally distributed.
mean = 24.2
Standard Deviation (SD) (delta) = 4.2
What is probability that a student scores greater than 31?
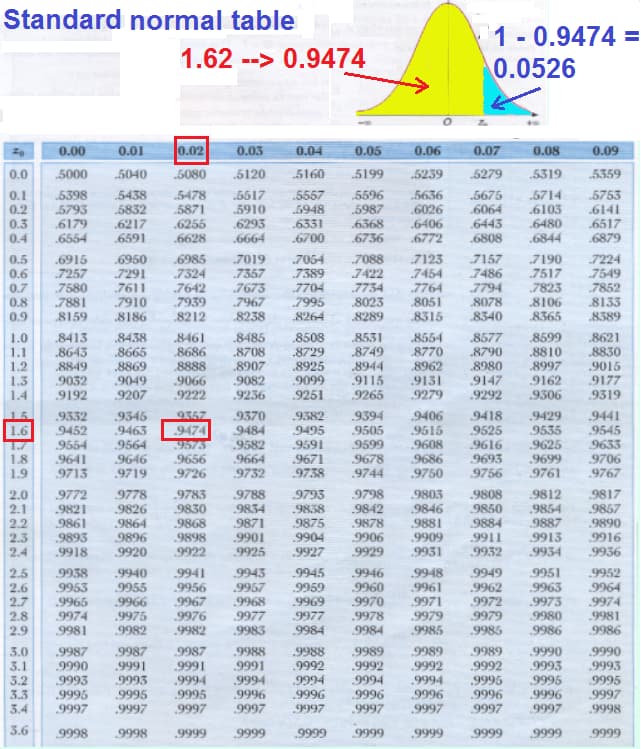
Use the Standard normal table.

Sol: the green area has a value of 0.0527, that is the probability.

Process:
a) To convert from a normally distributed x value to a z-score, we use the following formula:

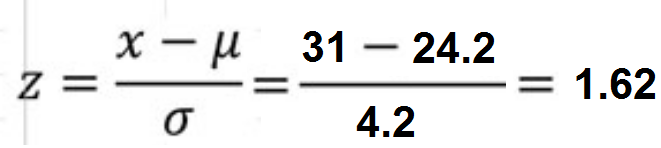
b) Now we consult the Standard normal table.

OOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO

- With Blocks.

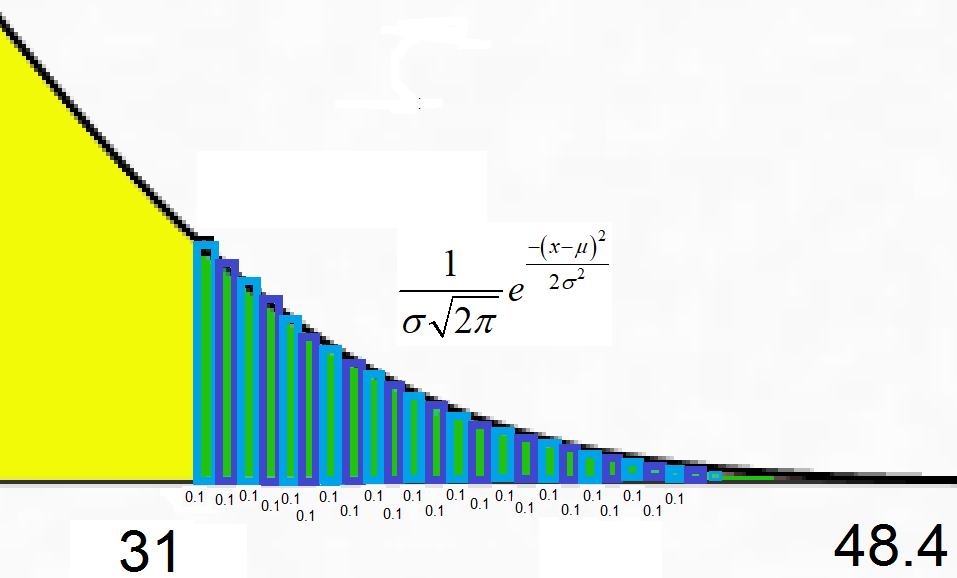
• Now we are going to calculate the area of ​​the green zone by another method.
  We will create small rectangles with a base of 0.1 and a height indicated by the function.
  
  
• We will add the area of ​​all those rectangles.

Through a "for" loop we are cumulatively adding the small rectangles (I have used a base rectangle of 0.01)

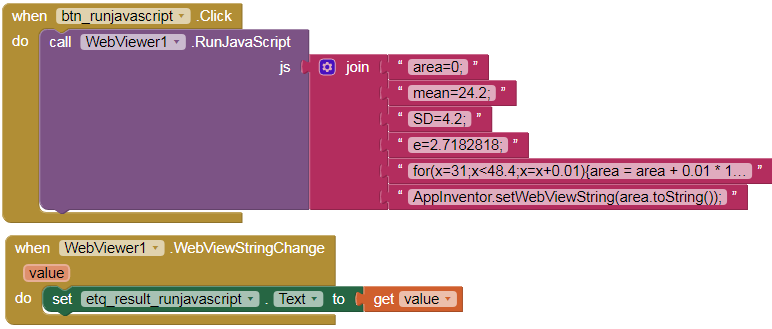
- With RunJavaScript of WebView component.

area=0;
mean=24.2;
SD=4.2;
e=2.7182818;
for(x=31;x<48.4;x=x+0.01){area = area + 0.01 * 1/(SD*Math.sqrt(2*3.1416))*Math.pow(e,Math.pow(x-mean,2)/(-2*Math.pow(SD,2)))};
AppInventor.setWebViewString(area.toString());

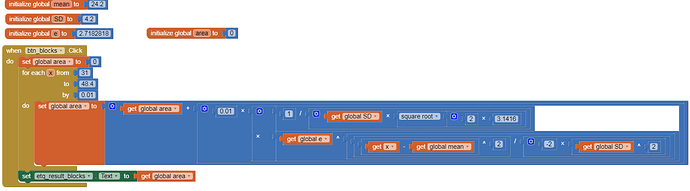
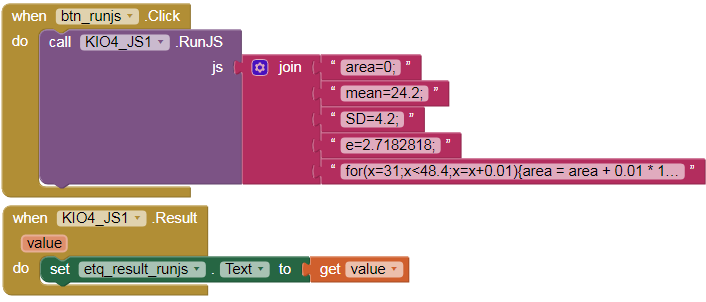
- With extension.

area=0;
mean=24.2;
SD=4.2;
e=2.7182818;
for(x=31;x<48.4;x=x+0.01){area = area + 0.01 * 1/(SD*sqrt(2*3.1416))*pow(e,pow(x-mean,2)/(-2*pow(SD,2)))};

- With extension. Insert block.
(It needs double click)

area=0;
mean=24.2;
SD=4.2;
e=2.7182818;
for(x=31;x<48.4;x=x+0.01){area = area + 0.01 * 1/(SD*sqrt(2*3.1416))*pow(e,pow(x-mean,2)/(-2*pow(SD,2)))};

Conclusion.

With blocks you get the slowest result. With JavaScript it is faster.
Even using a rectangle base of 0.0001, good speed is achieved in the result.
for(x=31;x<48.4;x=x+0.0001){area = area + 0.0001 *.....

With the insert block it is necessary to press the button twice.
You can get more accurate results by changing the base of the rectangles to 0.0001

• Another procedure would be to calculate the integral of the normal distribution, but the formula obtained is even more complicated.

[Juan_Antonio]

6.- Code proposal. Double factorial.

You know that the factorial of the number 9 is:

9! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = 362880

But, do you know that the double factorial exists?
Create an application to calculate the double factorial of an integer.

9‼ = 9 * 7 * 5 * 3 * 1 = 945

Double factorial

[ChrisWard]

Totally outstanding Juan.

[ABG]

Interesting!

[Juan_Antonio]

• Suggestion:: Calculate the PI value using formulas.

https://mathworld.wolfram.com/PiFormulas.html

[Spicy_Topics]

hello @Juan_Antonio , thanks for this wounderful extension...

BTW, how can i get result from this js?

function convertToDms(dd, isLng) {
  var dd =42.15188;
  var isLng = false;
  
  var dir = dd < 0
    ? isLng ? 'W' : 'S'
    : isLng ? 'E' : 'N';

  var absDd = Math.abs(dd);
  var deg = absDd | 0;
  var frac = absDd - deg;
  var min = (frac * 60) | 0;
  var sec = frac * 3600 - min * 60;
  // Round it to 2 decimal points.
  sec = Math.round(sec * 100) / 100;
  return deg + "°" + min + "'" + sec + '"' + dir;
}

console.log(convertToDms());

i have used the same code in both blocks but i get null.. instead of return i used out

ref link

[Juan_Antonio]

Try this:

; dir = dd < 0 ? isLng ? ' W' : ' S' : isLng ? ' E' : ' N'; absDd = abs(dd); deg = absDd | 0; frac = absDd - deg; min = (frac * 60) | 0; sec = frac * 3600 - min * 60; sec = round(sec * 100) / 100; salida=deg + "°" + min + "" + sec + "''" + dir;

dd =42.15188;
isLng = false;
dir = dd < 0
    ? isLng ? ' W' : ' S'
    : isLng ? ' E' : ' N';
absDd = abs(dd);
deg = absDd | 0;
frac = absDd - deg;
min = (frac * 60) | 0;
sec = frac * 3600 - min * 60;
sec = round(sec * 100) / 100;
salida=deg + "°" + min + "" + sec + "''" + dir;

[Spicy_Topics]

Perfect.. thank you man.. you are awesome.

[11124]

I don't understand why the launch of the simplest function only works for me the second time (i.e. every other time).
that is, when I run the execution again, it shows the result: (what could be the reason?

[Juan_Antonio]

It is a feature of this block, it needs double click.

[Kevinkun]

If you read the source code, you will know why.

The evaluateJavascript will return the value asynchronously. The result you get is the result of last time.
So the safe way is to use the Runjs and get the result in the Result event.

[11124]

the extension is really interesting and necessary.
it's a pity that such a feature. In fact, the need for such a block disappears.
and it's sad that all this works in the WebView component (I wanted to use this extension on a wearable device running Wear, but there is no android.webkit

[Juan_Antonio]

A workaround with a Clock.

borrar_runjs.aia (9.1 KB)

[Kevinkun]

You may want to use this extension.

App Inventor Extensions: Math Parser | Pura Vida Apps

[Neela_s_Kitchen]

Hey is it possible to use webrtc data channels using this extension the javascript code

// Creating a RTCPeerConnection object
const configuration = {}; // Configuration details for RTCPeerConnection

const peerConnection = new RTCPeerConnection(configuration);

// Creating a data channel
const dataChannel = peerConnection.createDataChannel();

// Listening for incoming data channels
peerConnection.addEventListener('datachannel', event => {
    const receivedDataChannel = event.channel;

    // Handling received data channel
    receivedDataChannel.addEventListener('message', event => {
        const receivedMessage = event.data;
        // Code to handle received message
    });

    receivedDataChannel.addEventListener('open', event => {
        // Code to handle opened data channel
    });

    receivedDataChannel.addEventListener('close', event => {
        // Code to handle closed data channel
    });
});

// Opening and closing events for the created data channel
dataChannel.addEventListener('open', event => {
    // Enabling elements when data channel is opened
    messageBox.disabled = false;
    messageBox.focus();
    sendButton.disabled = false;
});

dataChannel.addEventListener('close', event => {
    // Disabling elements when data channel is closed
    messageBox.disabled = true;
    sendButton.disabled = true;
});

// Sending a message when the send button is clicked
sendButton.addEventListener('click', event => {
    const message = messageBox.value;
    dataChannel.send(message);
});

// Receiving incoming messages and appending them to a message box
const incomingMessages = document.querySelector('#incomingMessages');

peerConnection.addEventListener('datachannel', event => {
    const receivedDataChannel = event.channel;

    receivedDataChannel.addEventListener('message', event => {
        const receivedMessage = event.data;
        incomingMessages.textContent += receivedMessage + '\n';
    });
});

[Spicy_Topics]

Hello all, i am able to sort this data using normal js but with this extension i feel to write the logic.

I tested with onecompiler and go the required output.

Input
const data = [
["17/12/2024", "ADA", 2180, "P1", 44100, 44100],
["17/12/2024", "ADA", 2100, "C1", 300, 29100],
["17/12/2024", "ADA", 2100, "P1", 55200, 314700],
["17/12/2024", "ADA", 2140, "P1", 75300, 64500],
["17/12/2024", "ADA", 2200, "C1", 5100, 196800],
["17/12/2024", "ADA", 2200, "P1", 77100, 395700],
["17/12/2024", "ADA", 1740, "P1", 11100, 57600],
["17/12/2024", "ADA", 1900, "P1", 7800, 111300],
["17/12/2024", "ADA", 2120, "P1", 4200, 61200],
["17/12/2024", "ADA", 2280, "P1", 87300, 108000]
];

// Sort the data by the 3rd element (index 2) in each sub-array,
const sortedData = data.sort((a, b) => {
const typeA = a[2];
const typeB = b[2];

if (typeA < typeB) return -1;
if (typeA > typeB) return 1;
return 0;
});

// Print the sorted data
console.log(sortedData);

when i run this i got the out put as i like..

Output:

[
[ '17/12/2024', 'ADA', 1740, 'P1', 11100, 57600 ],
[ '17/12/2024', 'ADA', 1900, 'P1', 7800, 111300 ],
[ '17/12/2024', 'ADA', 2100, 'C1', 300, 29100 ],
[ '17/12/2024', 'ADA', 2100, 'P1', 55200, 314700 ],
[ '17/12/2024', 'ADA', 2120, 'P1', 4200, 61200 ],
[ '17/12/2024', 'ADA', 2140, 'P1', 75300, 64500 ],
[ '17/12/2024', 'ADA', 2180, 'P1', 44100, 44100 ],
[ '17/12/2024', 'ADA', 2200, 'C1', 5100, 196800 ],
[ '17/12/2024', 'ADA', 2200, 'P1', 77100, 395700 ],
[ '17/12/2024', 'ADA', 2280, 'P1', 87300, 108000 ]
]

how to write the above js code to be fit with this extension???

[Spicy_Topics]

sorry, i found it and go the result. thank you

[ABG]

You know that AI2 added advanced sort blocks to the list block pallette, right?

We haven't seen you in a while.

[Spicy_Topics]

@ABG

advanced sort blocks to the list block pallette, right?

yes, i was away from the community due to personal reasons.

i will check it @ABG

thank you very much

[ABG]

FAQ Section: Lists

Introductory Making Lists (Concepts) - MIT Lists Chapter from MIT AI2 Online book Translatable copy of Lists Chapter from MIT AI2 Online book How to work with Lists - imagnity MIT AI2 List Blocks Help Page How to Display a List - MIT nb191 Advanced list blocks (filter, sort, map, reduce) Tables Dynamic-editable-html-table - @TimAI2 free-tableviewer-fully-style-customized-to-show-table-data (extension) - @Kevinkun Dynamic Table Layout and Table Listpicker (HTML) - @Taifun Samples (S…