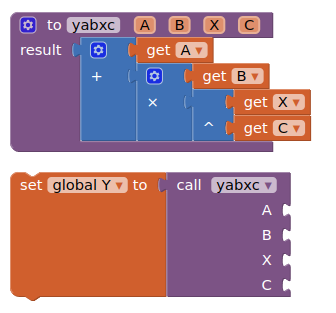
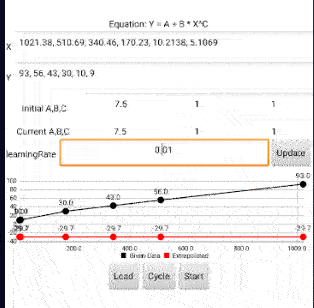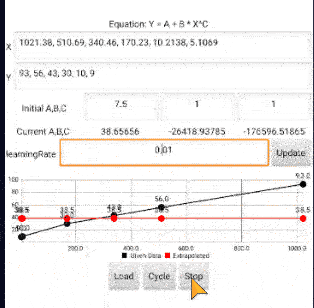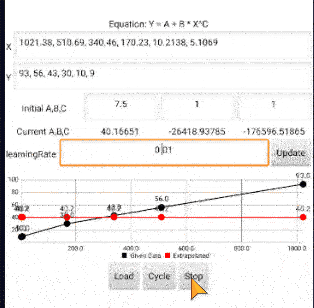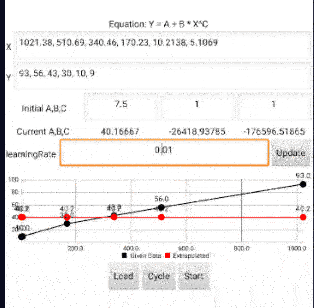
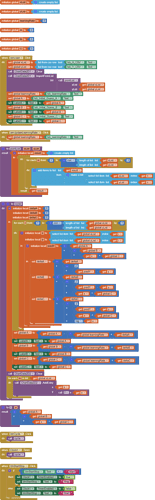
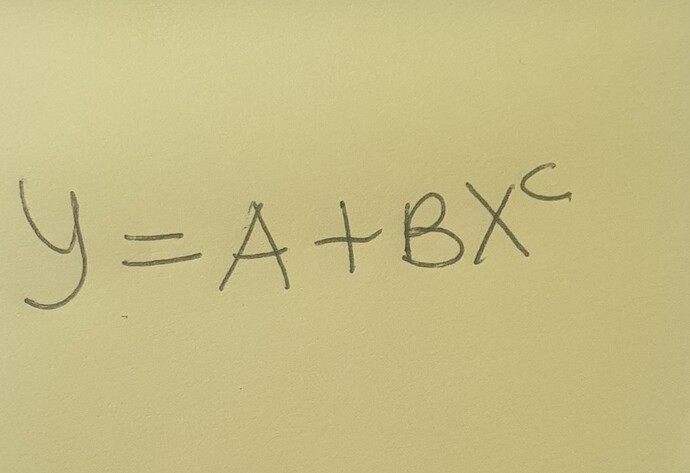Hello guys, I am trying to create an app that perform nonlinear curve fitting using nonlinear least square method. I can solve the problem with matlab and excel solver. Please I need help with using mit app inventor to solve same problem.
Matlab code below:
% Sample data
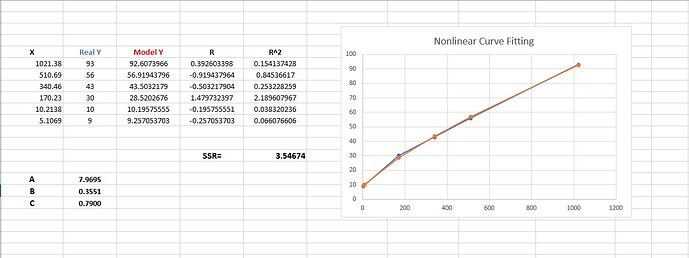
xData = [1021.38, 510.69, 340.46, 170.23, 10.2138, 5.1069];
yData = [93, 56, 43, 30, 10, 9];
% Initial guess for parameters [a, b, c]
initialGuess = [7.5, 0.7, 0.55];
% Define the function to fit (model function)
modelFunc = @(params, x) params(1) + params(2) * x.^params(3);
% Set lower and upper bounds for parameters [a, b, c]
lb = [-inf, -inf, 0]; % Lower bounds (set c >= 0 to ensure it remains non-negative)
ub = [inf, inf, inf]; % Upper bounds
% Use lsqcurvefit to fit the model to the data
estimatedParams = lsqcurvefit(modelFunc, initialGuess, xData, yData, lb, ub);
% Extract the estimated parameters
a = estimatedParams(1);
b = estimatedParams(2);
c = estimatedParams(3);
% Display the results
disp(['Estimated Parameters: a = ', num2str(a), ', b = ', num2str(b), ', c = ', num2str(c)]);
% Plot the data and the fitted curve
xFit = linspace(min(xData), max(xData), 100);
yFit = modelFunc(estimatedParams, xFit);
figure;
plot(xData, yData, 'o', 'DisplayName', 'Data');
hold on;
plot(xFit, yFit, 'r-', 'DisplayName', 'Fitted Curve');
xlabel('x');
ylabel('y');
legend('Location', 'best');
grid on;
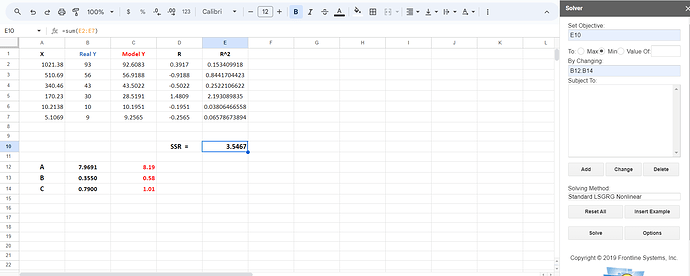
Excel gave same result: