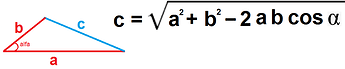What an excellent library of exercises! Thanks for sharing it!
20.- Minimun surface.
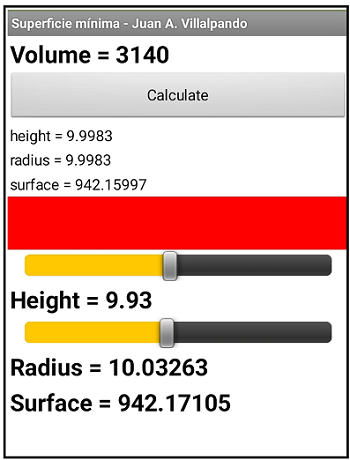
An open-topped cylindrical container has a volume of V = 3140 cm3. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container.
From: https://www.hackmath.net/en/math-problem/5891?tag_id=91&result=1

- Build an application using the expressions above.
- And with two sliders that move them calculate the surface keeping the volume constant. Check the minimum surface, in this case 942.16
apk file in external link: http://kio4.com/appinventor/apk_archivos.htm
On this website you can find many mathematical problems:
21.- Maximun angle.
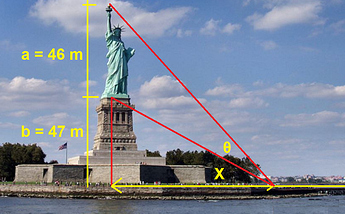
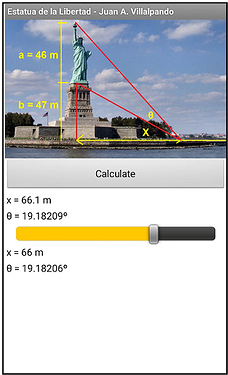
The Statue of Liberty measures 46 m, is 47 m above ground level, look image.
What distance should one stand away from the statue in order to maximize the view of the statue? That is, what is the maximum angle Θ.
-
Build an application using the expressions above.
-
And with a Slider change value of x, get Θ and check the maximum angle Θ, in this case Θ = 19.18209º to x = 66.1 m
-
Information: https://www.slideshare.net/leingang/lesson-20-more-optimization-problems (pag. 20)
-
apk file in external link: http://kio4.com/appinventor/apk_archivos.htm
22.- Law of cosines.
In a right triangle we can calculate the c side using the Pythagorean theorem.
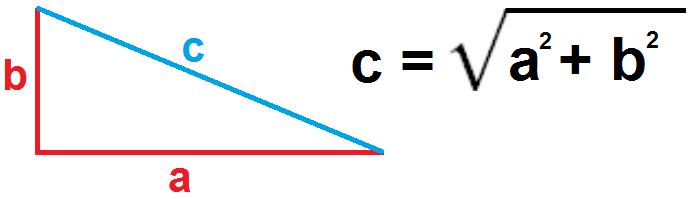
If the triangle is not a rectangle, we can calculate the c side using the Law of Cosines.
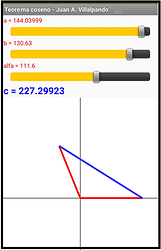
Build an application where you can change sides a and b and the alpha angle using Sliders and get side c. Draw the triangle.
apk file in external link: http://kio4.com/appinventor/apk_archivos.htm
teorema_cosenos_i.aia (3.6 KB) (unfinished)
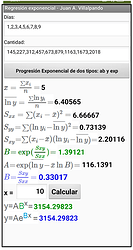
23.- Exponential regression.
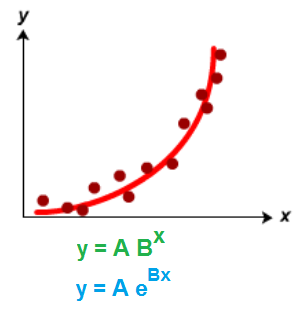
Create an application to obtain the expression of an ab-exponential and e-exponential regression.
- ab-Exponential regression. ![]()
You can get information about the ab-exponential regression in:
- e-Exponential regression. ![]()
You can get information about the e-exponential regression in:
apk file in external link: http://kio4.com/appinventor/apk_archivos.htm
p84F2_regresion_exponencial_i.aia (30.2 KB) (unfinished)
@Juan_Antonio outstanding job with these. Please continue to share. AI2 community is very lucky to have you contributing work of your quality. God bless 
Hi, with this apk is possible calculate a integral of a real number? for example int(0,74)? tks
This is an integral
24.- Calculate PI.
Create an app to calculate the value of PI with many decimals.
The output should be a decimal sequence beginning 3.14159265 ...
25.- Find the division between two numbers by repeatedly subtracting the dividend minus the divisor.
Example: 22 / 4

- Don't use JavaScript
- Here with JavaScript: p167G_javascript_division.aia (4.3 KB)
hello, great demonstration !!!
if I take your first example on calculating the area of a polygon, is it possible to color it?
what is the method (I am not as efficient as you in this field, I would even say beginner :-))
Thanks for reading
perhaps see here:
A post worth bookmarking, not just for App Inventor but also if you need help with Maths 

26.- Cistercian Numerals.
Write a decimal number from 1 to 9999 and convert it into a Cistercian number.
Cistercian number: http://www.davidaking.org/Ciphers.htm
p91G_cisterciensesi.aia (19.3 KB)
[not finished. It contains the 36 images of the symbols, with a transparent background.]
Did you watch this? 
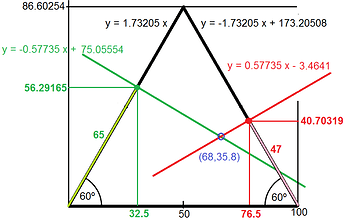
27.- Find the crossing point of two lines perpendicular to two sides of an equilateral triangle.
apk file in external link: http://kio4.com/appinventor/apk_archivos.htm
We have an equilateral triangle whose sides are 100.
On the left side we draw a segment of 65 and on the right side another of 47.
Find the equation of the line that passes through these points and is perpendicular to the sides.
Find the point where these lines intersect.
This triangle is used in various problem domains, from describing earth samples based on their proportions of sand, clay, and silt (a recent question on this forum) to choosing newly created character attribute values in the game Fallout 4 (according to my son (I haven't reached that game yet.))
The equilateral triangle has the interesting property that any point within the triangle's closest distances to the the three sides always add up to the same number, the height of the triangle.
Unfortunately, no source code is here, so we have to derive the equations from scratch.