Our current subject in class is using procedures made in the Logo app demonstration.
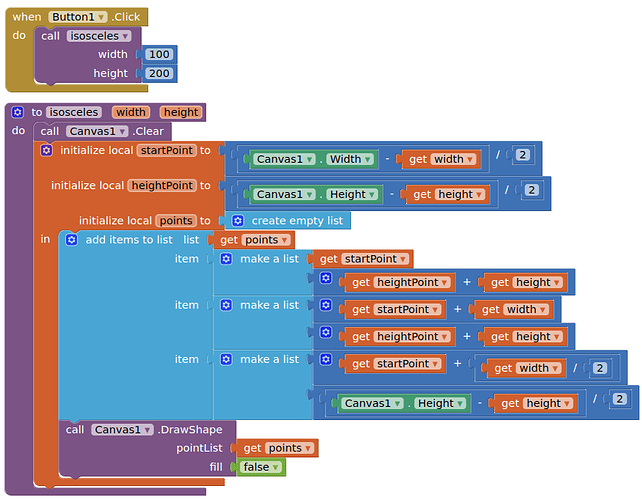
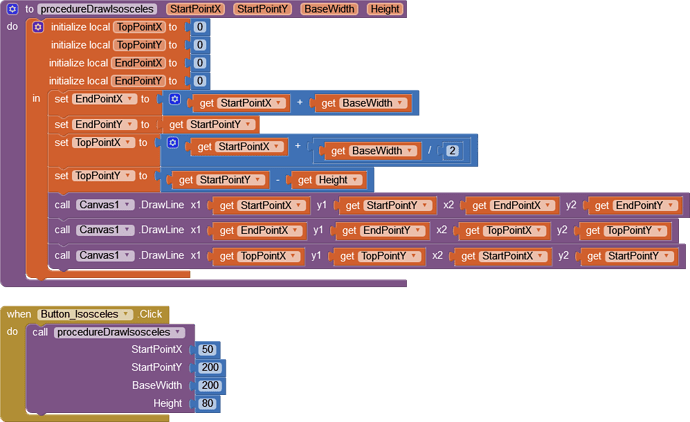
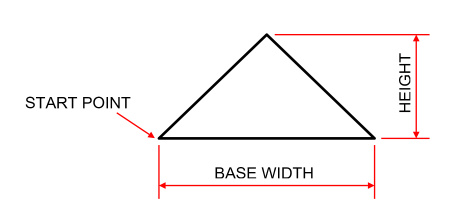
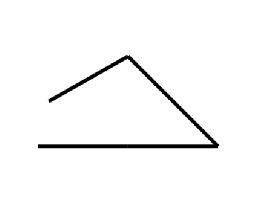
I'm really struggling with triangles, and I'm not sure what I'm missing. Currently my objective is to make an isosceles triangle. My results almost always end in the left and final side of the triangle drawn with a slight gap between it and the start point.
Math is a weak point for me, so did have to re-google some of it. Feel free to call out algorithm errors.
That being said, here's the methods I've tried:
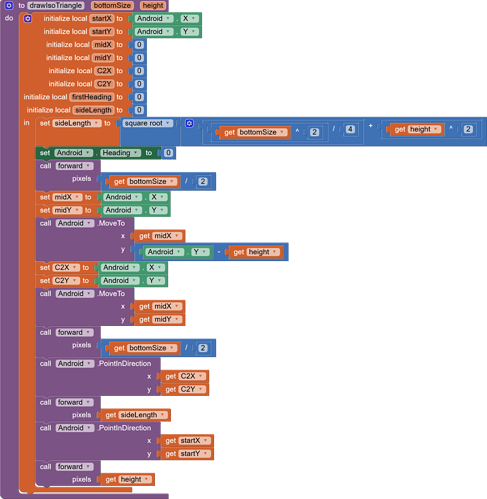
-First line is the base drawn straight based on a bottom length variable, the next angle I tried to base the top corner by taking the X value of the current X/Y and reduce it by half of the base length. Then I have a separate height value which I reduce the Y value by to generate an X/Y I can then point the sprite towards and draw the next line.
A problem with the first method is the first line almost never came out tall enough.
-Next attempt I started looking into math such as Pythagorean. Unfortunately I've never been versed in trig, and saw a lot of options that way but I feel like this is way more than I should need in this example. My goal this time was using a^2 = sqRoot(b^2/4 + c^2) since I have not figured out a way to get the direction degrees outside of capturing heading. So I used this formula to calculate what would be the side length based on the height and base values. This result comes a little closer but ultimately is the same issue.
This is what usually occurs on almost any method I've tried.
Here's what I currently have. Everything else is stock. Edit: The last forward should be get sideLength. Just noticed and changed it with no impact.
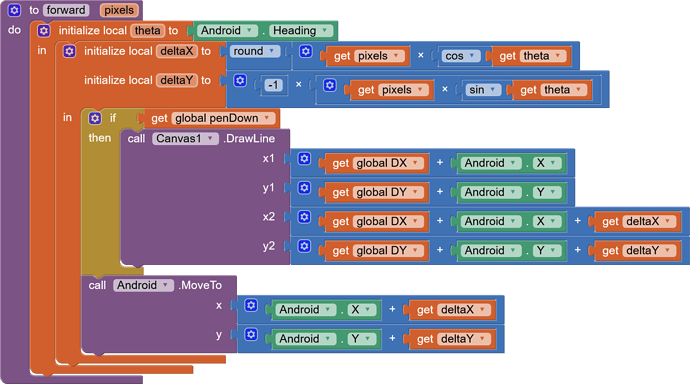
And in case you're not familiar with the project, here's the main snippet being used:
Even using the app by default with no changes, regular triangles from the included drawTriangle procedure break once they come anywhere close to the edge of the canvas or are large in general.
The end goal project is just drawing a house, I've gotten everything else but the roof which will be this isosceles triangle.