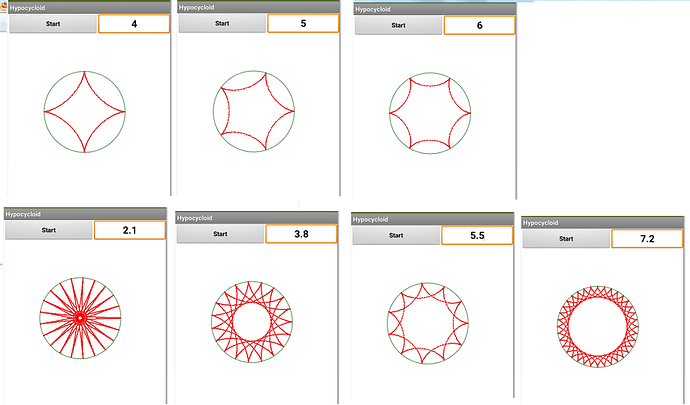
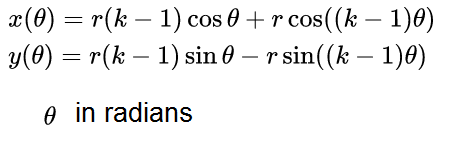28.- Mathematical proposal for Pi day.
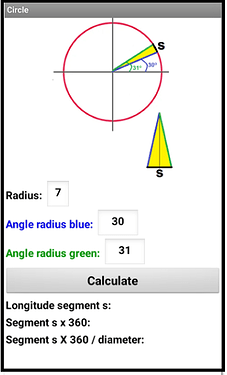
A circle has radius 7. We draw a radius at 30º and another at 31º, as the schematic figure indicates.
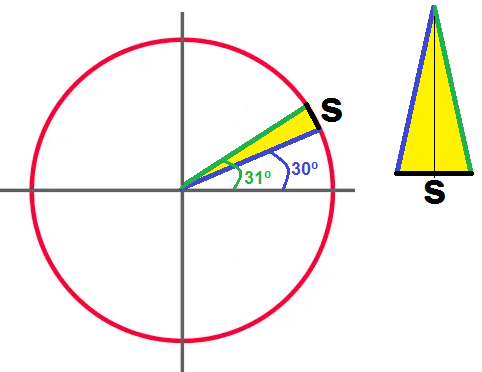
a) Find the value of the segment s.
b) What is the sum of the 360 segments s drawn on the circle?
c) What value do we obtain by dividing the previous sum by the diameter of the circle?
d) Carry out the previous sections when the radius are 0.1º apart.
29.- Abacus Clock.
This "Abacus Clock" application indicates the actual time: HHMMSS.
It is a good idea to do it with App Inventor.
https://apkpure.com/clock-abacus/appinventor.ai_mydigitaldesk.clock_abacus
30.- Validate Credit Card.
Write an application where the user enters a credit card number and shows if that card is valid or not.
Use the Luhn algorithm:
http://www.brainjar.com/js/validation/default2.asp
Can you please tell where can I download extension?
Thank you @Juan_Antonio
I tried to find in your website before I posted. But could not find the extension!.
Thanks for your help.
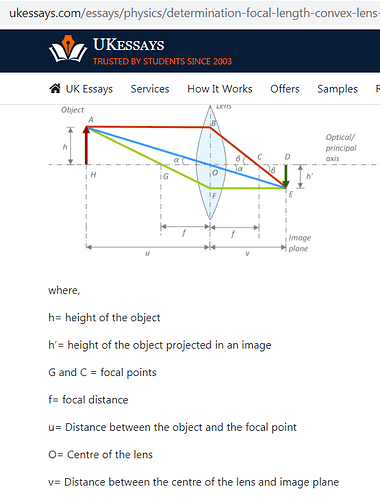
31.- Optical. Calculation of the scale of an image (beta).
-
On this page we can find information about the calculation of lenses:
https://www.ukessays.com/essays/physics/determination-focal-length-convex-lens-5760.php -
Here an application from the Play Store to perform physics calculations:
https://play.google.com/store/apps/details?id=de.ejbguru.android.formulaApp&hl=es&gl=US
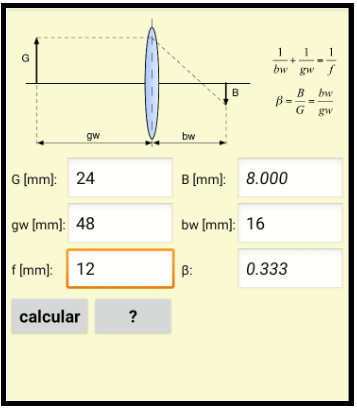
Build an app where you enter the height of the image (G), the distance between the image and the axis of the lens (gw) and the focal length of the lens (f), and obtain the height of the projected image (B ) and the image scale (beta = B / G)
Simulator online (move Focus').
Thank you so much I needed this for my physics practice.
32.- Encode and decode a string using Base 45.
...Base-64 should be a well-known format, and often used to convert binary data into a text format. In Bitcoin, we use Base-58 for the Bitcoin address. But, what is Base-45?
https://billatnapier.medium.com/so-what-is-base-45-and-where-is-it-used-1ab53279d705
https://datatracker.ietf.org/doc/html/draft-faltstrom-base45-03
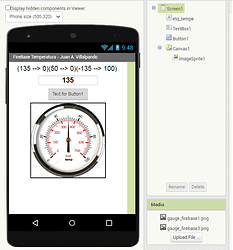
33.- When we write a number from 0 to 100, in the Textbox, the needle must mark that value in the Gauge.
- You must find the equation of the line that converts the values 0 and 100 to 315 and -315.
p91B_gauge.aia (169.8 KB) (unfinished)
34.- Swap two numbers without using a third variable.
Now
a = 9.85
b = 2.22
After
a = 2.22
b = 9.85

p87Ci_variables.aia (2.3 KB) (unfinished)
35.- Draw a cycloid curve.
Ecuations:
x = r (t - sin t)
y = r (1 - cos t)
t in radians.
-
Cycloid: Cycloid - Wikipedia
-
A Cycloid is a Tautochrone curve: Tautochrone curve - Wikipedia
( is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve.) -
Build a Tautochrone Track:
Tautochrone Track - YouTube
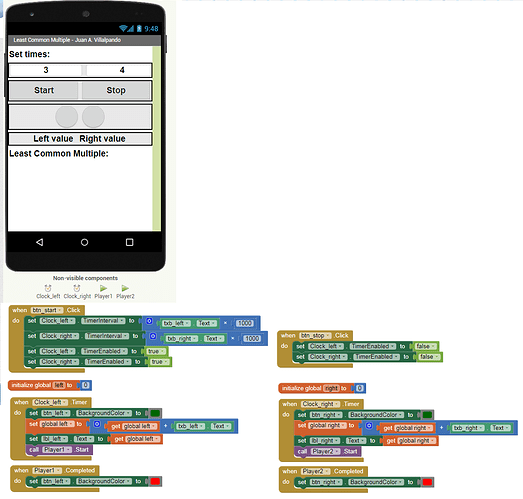
37.- Find the least common multiple of two numbers.
mcm.aia (9.9 KB)
A lamp blinks and play a sound every 3 seconds.
Another lamp blinks and play a sound every 4 seconds.
Calculates the time to first match (LCM).
38.- Calculate Julian Day and Julian Date (with Blocks).
The Julian calendar, was proposed by Julius Caesar 46 [BC]. Roma. Solar.
The Gregorian calendar is a modification and replacement of the Julian calendar. Salamanca 1582. Solar.
And this is Julian day. (JD) (Converter)[Today 23 July 2022 is JD: 2459784]
Julian DAY == The interval of time in days since noon at Greenwich on 1 January 4713 BC
Julian DATE == The day number within the year counting January 1st as 1 and December 31st as 365 (or 366 in leap years).
39.- Convert Julian Day to Gregorian calendar.
In this topic, you can see a code with JavaScript functions to convert a date to Julian Day and Gregorian calendar, adapt that code to App Inventor Blocks.
Use the following functions:
function mod(a, b)
function leap_gregorian(year)
function gregorian_to_jd(year, month, day)
function jd_to_gregorian(jd)
Easier with the expressions you can find in:
https://en.wikipedia.org/wiki/Julian_day
and WebViewer.RunJavaScript
40.- Magic square 3x3.
- Write a number less than 100, example: 25
- Show that number and the next 8: 25, 26, 27, 28, 29, 30, 31, 32, 33.
- Using a formula, calculate the magic constant of those numbers in a 3x3 square. It is 87.
- Place those numbers in the 3x3 square so that the sums of each of its rows and columns give the magic constant, in this case 87.
41.- Calculation of magic, neon and automorphic number.
- Using only blocks calculates...
a) Magic numbers less than 500.
https://pencilprogrammer.com/python-programs/magic-number/
b) Neon numbers less than 500.
https://pencilprogrammer.com/python-programs/check-neon-number/
c) Automorphic numbers less than 500.
https://pencilprogrammer.com/python-programs/automorphic-number/
- Build the same application using JavaScript.
42.- Golden Ratio in a 3x3 Square
A circle is drawn on a 3x3 square that measures 12 cm on each side. Calculate the radius of the circle.
Observe the figure.
What is the value of the golden ratio.
https://www.cut-the-knot.org/do_you_know/3x3GoldenRatio.shtml