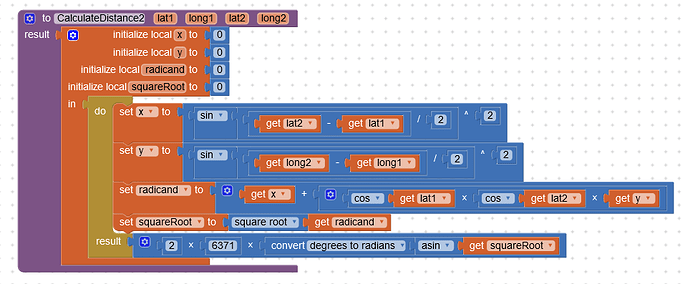
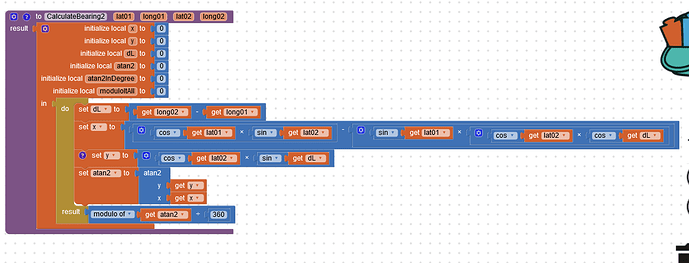
So I wanted to calculate the distance and bearing of two locations, given their latitude and longitude. I finally succeeded in it, but it was a wild ride to get there and here is why:
All the formulas I found on the internet that explained how to code said behaviors in javascript and how to implement it in excel, said to first convert tatitude and longitude from degree to radians. And they said to convert the result back to degree in the end. I struggled with the formulas for a long time because I did not get the correct results. I thought I entered the formulas wrong or had wonky decimals. Then I broke the formula down in tiny steps and displayed every step on the way to the result. I was surprised when I noticed by accident that in App Inventor, I did not need to convert latitude and longitude before doing anything with them. If I converted them, they'd deliver wrong results. I assume the operations somehow convert them before continueing their work.
I wonder why, because if that is supposed to be a comfort feature, I found it to be more hindering than comforting, because the formulas I found on the internet did not work. I also did not see it mentioned in the description of the math operations or anywhere.
I figured it out in the end so I do not have a problem anymore but if anyone stumbles across this problem in the future, hopefully you'll find my post and save some time.
Edit: I found that I used a formula from another topic that DOES convert radians to degree in the end and now I am more confused then ever. Anyways, the screenshots I attached do work for calculating distance and bearing, I doublechecked with this webpage: Calculate distance and bearing between two Latitude/Longitude points using haversine formula in JavaScript
Edit2: cleaned up screenshots, they contained unnecessary blocks