Knight moves and list errors

[cocoescoloco]

Hi,
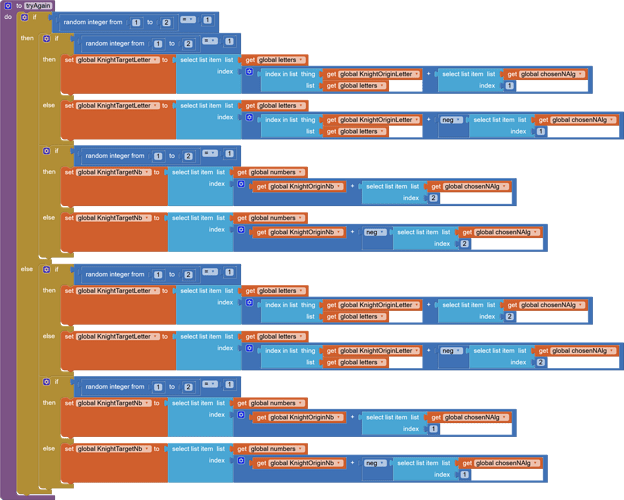
I am trying to build an app to develop board visualization in chess. One exercise lets the user choose a number of moves for a knight to go from one random square to another. The target position is set using a list of algorithms. For example, in two moves, a knight can go to a square reached by moving one square on any axis, and two squares in the other. So I thought I could offset the X and Y of the starting square by randomly choosing between (1,2) , (-1, 2), (2, 1), (-2, 1), etc. The X and Y axis are a list of the letters a to h and a list of numbers 1 to 8.
Of course, in doing so, my procedure often returns errors like: looking for index -2 in a list, or index 9 in a list of 8.
I thought I could get away by restarting the procedure (with a while block) until it selects a square within the board, but that doesn't seam to work.
How should I rearrange my procedure in an efficient way? While navigating in the indexes of a list, should I always check that I won't exceed its lenght? Or is there a simplier way to navigate my chessboard matrix?

[ABG]

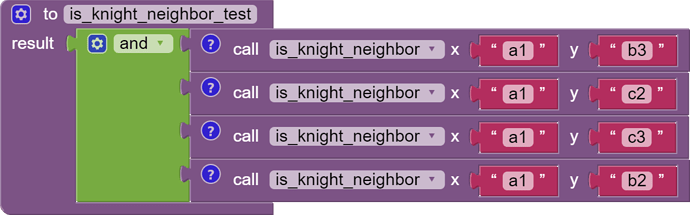
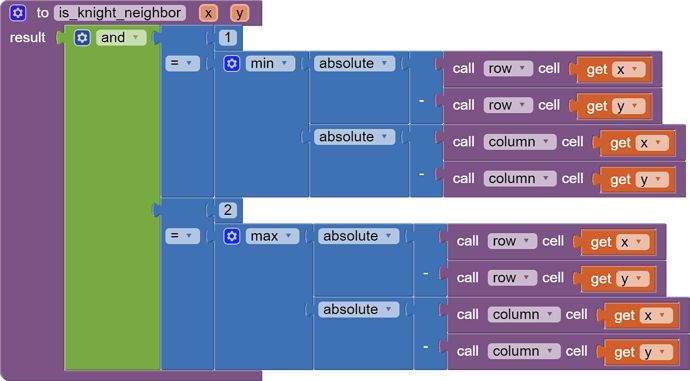
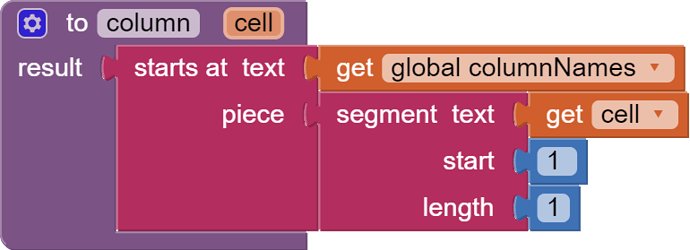
There is a board notation for chess that names each square alphanumerically, like spreadsheet cells.

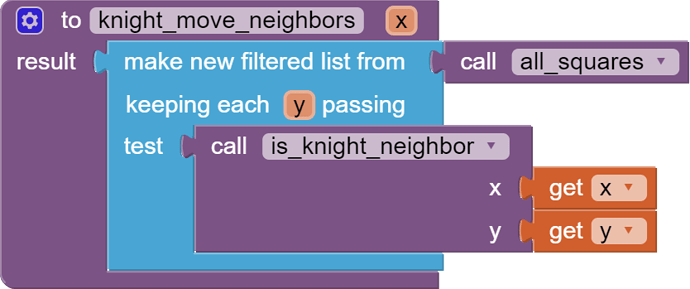
That makes it simple to predefine a dictionary KnightNeighbors with square name as key and list of knight move neighbors as value.

If you are showing the board as a Label matrix you could keep a dictionary mapping square names to to component blocks.

[cocoescoloco]

Thank you for your reply!

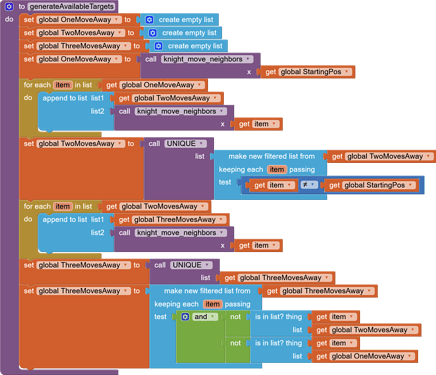
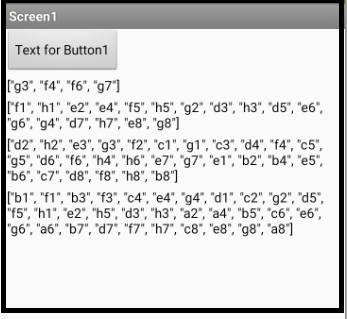
My game is to guess a possible path to reach a square in 2, 3, or 4 moves, starting from any of the 64 squares. Manually predefining a dictionary with all accessible squares for all 64 possible starting squares looks like a lot of manual work to me! (a bit less than 64x64=4096 solutions)

Surely there must be a more practical solution...

[ABG]

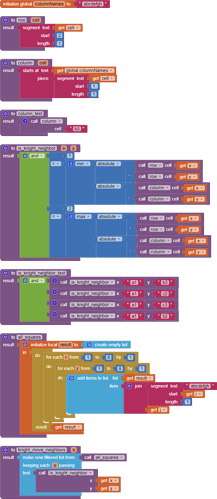
Value procedures are handy ways to hide complexity, if you compose them.
knight_moves.aia (3.9 KB)

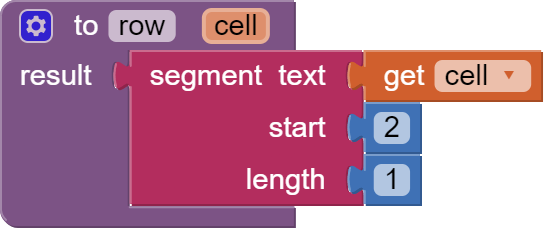
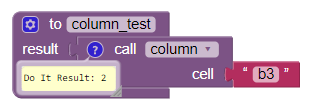
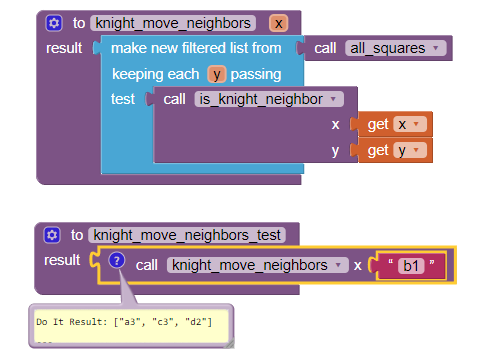
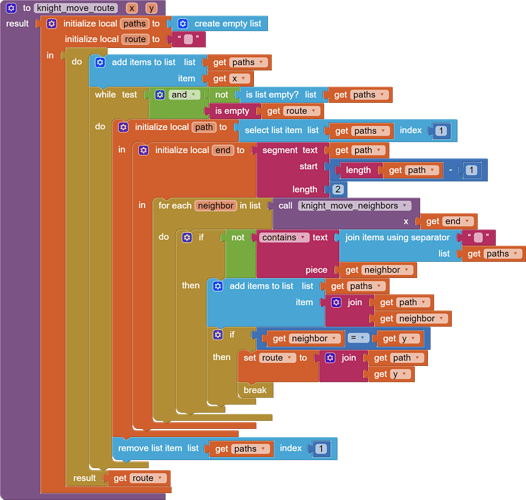
knight_moves.aia (4.0 KB)

It is possible to go further with this approach using recursion.
Interested?

[cocoescoloco]

Thank you so much for such a thorough answer! Of course I'm interested!
I will need a little time to fully grasp what you did there, as I'm not familiar with procedures returning a result. I will then come back here if I have any questions. I guess using recursion would be a way to list neighbors of neighbors, is that what you meant?

[ABG]

Okay, I will take a whack at it. In the meantime, search the Web for Dijkstra's Algorithm.
(From my phone)

[cocoescoloco]

Thank you,
as I understand it, Dijkstra's Algorithm is a way to find a shortest path, which I don't think I need.
I plan to:

• let the user choose a number of moves (n= 2, 3, or 4)
• pick a random starting square (x)
• pick a random target square (y) from the list of squares the knight can reach from (x) in (n) moves ("neighbors of neighbors")
• let the user state one possible path from (x) to (y) in (n) moves (without seeing the board), using speech recognition
• check if it's a valid answer: I guess I only have to check that every step is a valid knight move ("neighbor") and that (y) is the (n)th move .

So I think I'm good with what you gave me, no need for a shortest path.
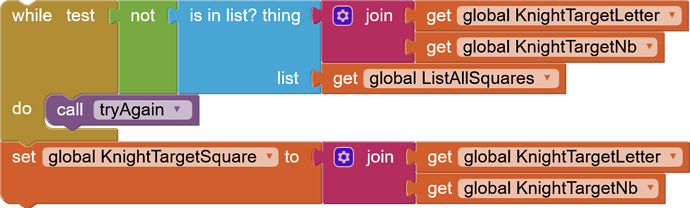
This is what I did to list the "neighbors of neighbors". Not very elegant, but it seems to work

[Juan_Antonio]

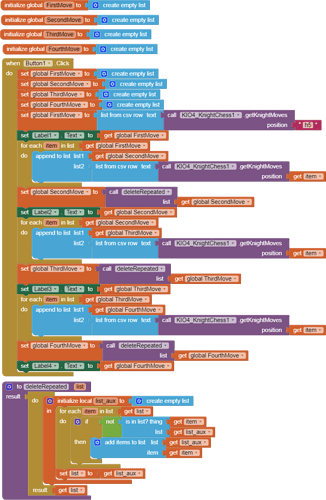
Using an extension (thanks to GPT), I have made this code.
If you set a starting position, it shows the positions where the chess knight can be placed.
4 movements are shown.

Ajedrez_Caballo.aia (8.2 KB)

com.KIO4_KnightChess.aix (5.4 KB)

[With this extension, you write a position and get the possible positions of the chess knight.]

[Related: https://community.appinventor.mit.edu/t/so-temp-ban-on-chatgpt/84903/5]

[ABG]

knight_moves.aia (5.6 KB)

I had to get this off my chest.

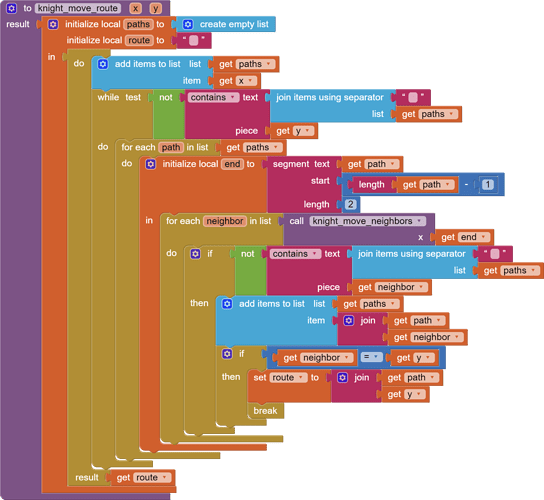
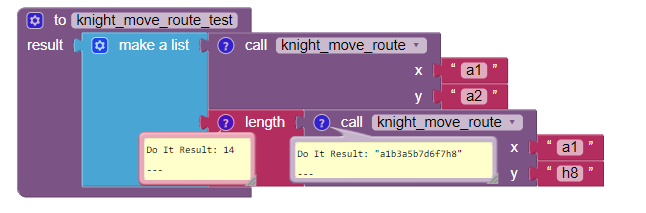
Here's a shortest path procedure that will return the shortest path in knight moves from one cell to another. Number of moves is (text length of path)/2 -1.

Note: If there is no route, this algorithm is not smart enough to stop looping.

[Juan_Antonio]

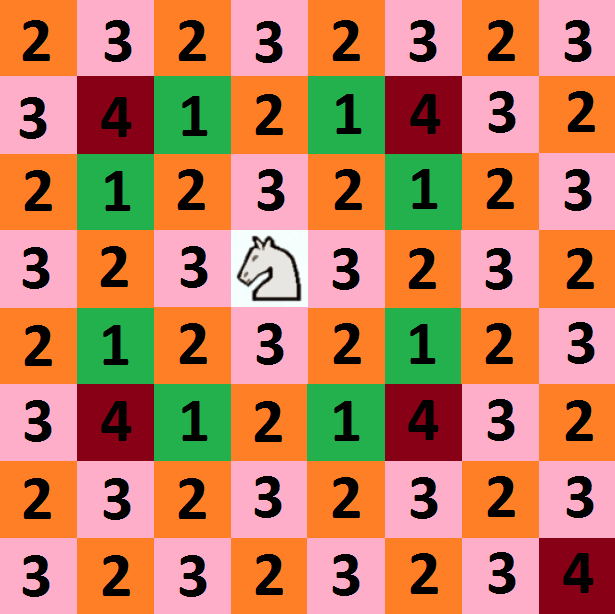
In this version we establish a starting square, for example b1 and we obtain the places where it can be at the "ThirdMove".

• We can change "ThirdMove" to "FourthMove" in the color process.

Ajedrez_Caballo_2.aia (12.4 KB)

[ABG]

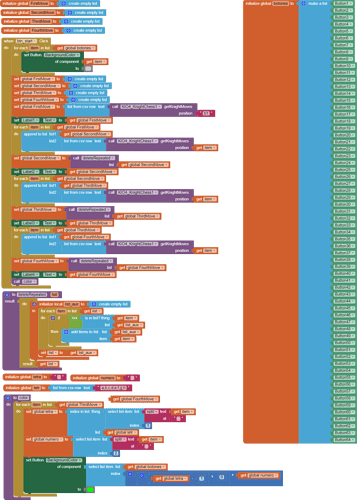
Here is a corrected version of the shortest route code I posted earlier, that

• terminates regardless of nonexistence of any route
• gives the shortest route.
  
  
  
  
  knight_moves.aia (6.0 KB)

[cocoescoloco]

Horses are smart creatures! they always find their way to any square.There is this mathematical problem, called Knight's Tour, in which the knight has to travel to every square on the board:

Knight's tour

I don't understand how your program chooses when there are several paths of the same length, as is often the case. Does it stop at the first correct answer?

[ABG]

@cocoescoloco

Does it stop at the first correct answer?

Yes. It does a breadth first search, checking all shorter paths before starting to check longer paths.