How to check prime numbers?

Tutorials and Guides
,
1

Today we will learn about checking prime numbers, in App Inventor. It is possible to check, without any APIs and extensions. Let's start!

A prime number is a number that is only divisible by 1 and the number itself.

  1. Create some project
  2. Structure (not design) should be like this:

bcghd
bcghd342×509 11.7 KB

Don't forget to make textbox Numbers Only, because it will throw an error when user types text instead of number!

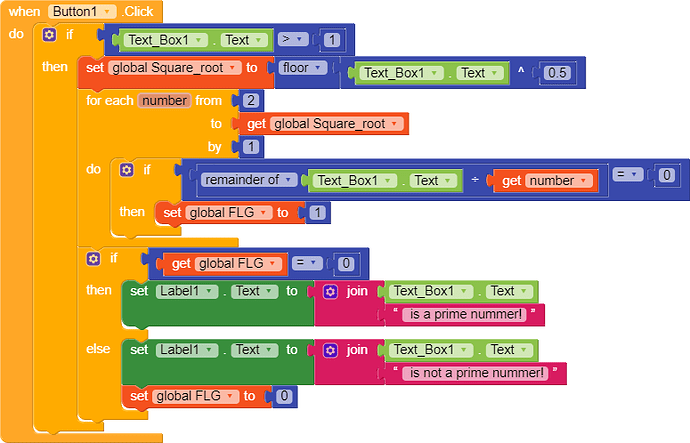
Let's move on to blocks!

First, we declare a Boolean-typed flagging variable, with value of 0. I called it FLG.
We'll not use True / False blocks for better understanding.

df

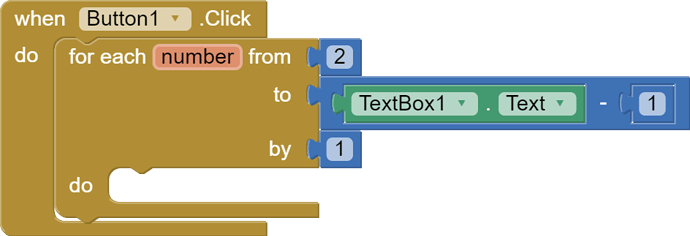
Next, we add a For block in button1.click or any other button.

We are starting from 2, because it is the first prime number. But 1 is also but it isn't considered.

We are writing Textbox1.text minus 1 because it is the best way to check, and also if we enter a non-prime number, it will say accordingly since it is divisible by the loop.

blocks
blocks944×324 24.9 KB

Next we add an if then block inside that For loop!

We will be checking the remainder of Textbox1.txt ÷ The loop number

If 0, then it is not prime, and FLG is set to 1.

blocks (1)
blocks (1)1340×182 27.3 KB

Now the final part! If FLG is 0 then show it's prime else not prime.

!!! VERY IMPORTANT !!!
Set FLG to 0 otherwise it'll show the message 'Not a prime number' even if it's a prime number!

blocks (3)
blocks (3)1112×660 95.9 KB

All is ready!

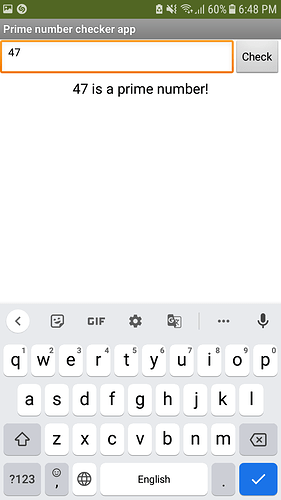
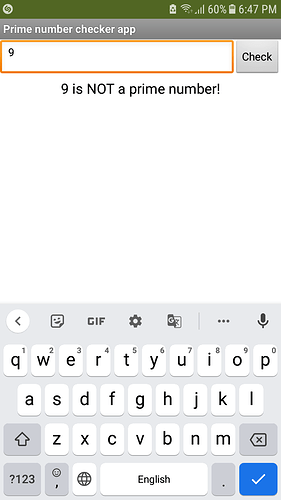
Output

Screenshot_20220804-184811
Screenshot_20220804-184811720×1280 59.1 KB

Screenshot_20220804-184742
Screenshot_20220804-184742720×1280 59.3 KB

Thank you! Further improvements are always welcome!

Feel free to reply!

2

You don't explain what a prime number is in your tutorial.

1 Like
3

Explained it!! :slight_smile:

4

Try your solution with a large number like
429762337057011941556865358029
(taken from here https://bigprimes.org/) and let us know what happens and why...

Taifun

1 Like
5

The rational square root of a rational number, if any, is the largest factor of that number that is less than itself. So to scan prime numbers, it's enough to take the square root of a number, and that will reduce our trading volume tremendously. Thanks for your sharing. I've improved a bit what I learned from you.

blocks - 2022-08-04T224923.626
blocks - 2022-08-04T224923.626775×498 43.3 KB

5 Likes
6

It will simply crash the app.

Because of the For Each block and the procedure isn't meant to calculate such large prime numbers.

7

Use Goldbach's Conjecture:

Or you can provide some good approach to cover very large number aswell. Example :

2 Likes
8

You forgot to mention, that there is such a restriction with your tutorial...
What about providing a solution, which also works for large numbers?
Tip: try alogic, which uses a clock component to avoid the runtime error...

Taifun

2 Likes
9

Also, in this traditional approach aswell,
you may break the loop if you found out number is divisible by something..

FOR i = 2 TO (n-1) DO
    IF(n%i == 0) THEN
        FLG = 1
            break;
1 Like