The Eratosthenes experiment March 2021 will take place on the first working day after the March equinox day, Monday the 22nd of March. You can perform the experiment in collaboration with another school that shares the same longtitude or if no other schools can be found on the same longitude - for your matchup – you can consider the existence of a virtual school on the equator with experimental data 0 (shade of a one-meter stick measured at local noon) and conduct the experiment by yourself.
https://eratosthenes.ea.gr/
Here are two simple proposals to do with App Inventor:
1 Like
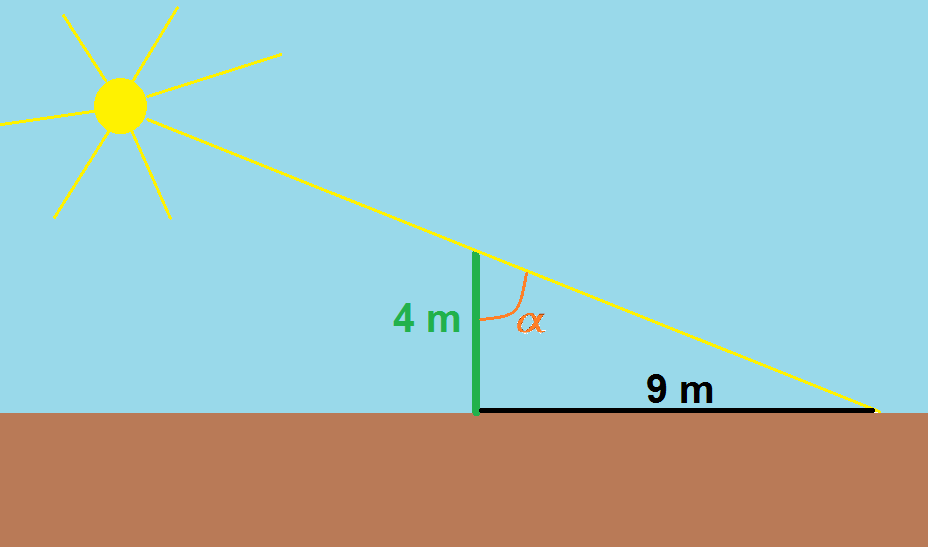
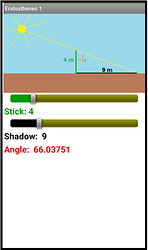
1.- The stick measures 4 m and its shadow 9 m. Find the alpha angle.
1 Like
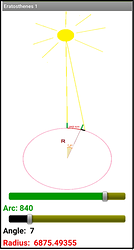
2.- The arc measures 843 km and the angle 7.2º. Find the Radius of the circle.
1 Like
3.- Zero shadow day.
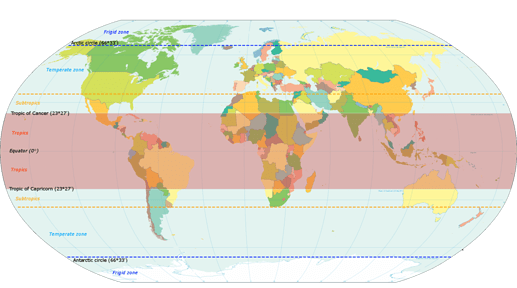
A zero shadow day is a day on which the Sun does not cast a shadow of an object at noon, when the sun will be exactly at zenith. Zero shadow day happens twice in a year for the places between +23.5 and -23.5 degrees of latitude. (From Wikipedia).
Shown here is the area on Earth between the Tropic of Cancer and the Tropic of Capricorn where there may be a day or two with zero shadow.
(Image from:
https://commons.wikimedia.org/wiki/File:World_map_indicating_tropics_and_subtropics.png)
1 Like
4.- Carl Sagan explains how Eratosthenes circumference of the Earth.
In this famous documentary, Carl Sagan tells us that "there was no shadow at Syene (today Aswan)", it is strange because it is in the Tropic of Cancer and there are only one or two days with zero shadow a year, possibly there was shadow in Syene when Erathostenes made his measurements.
Therefore we are going to perform the calculation when there is shadow in both positions...
1 Like
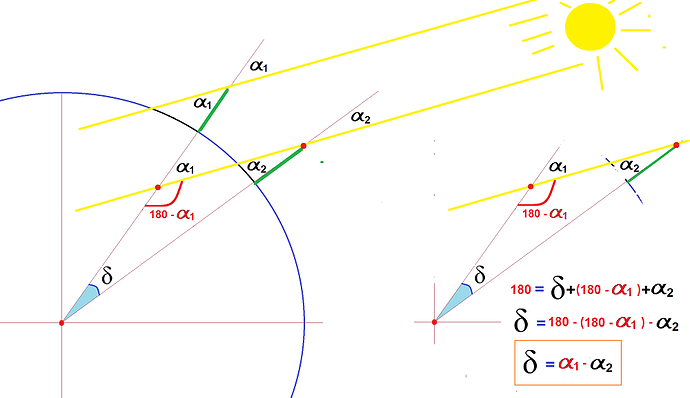
5.- Two places, two shadows. Playing with angles.
- In the graph, we know alpha1 and alpha2. Find the delta angle.
- Observe the triangle with vertices of red points, in a triangle the sum of its angles has a value of 180º.
1 Like
6.- We are going to calculate the radius of the Earth from our house...
We will put a stick of 1 m in Alexandria and measure its shadow at 12 o'clock today. We will calculate the solar angle alpha1.
Then we will put another stick of 1 m in Syene (today Aswan) and measure its shadow at the same time. We will calculate its solar angle alpha2.
When we have these two angles we will calculate the delta angle.
The distance between Alexandria and Syena (Aswan) is 843 km, we can measure it using Google maps.
How can we calculate it?...
...with this simulator:
Alexandría: Stick 1 m. Shadow: 0.60 m, .... alfa1: 30.96º
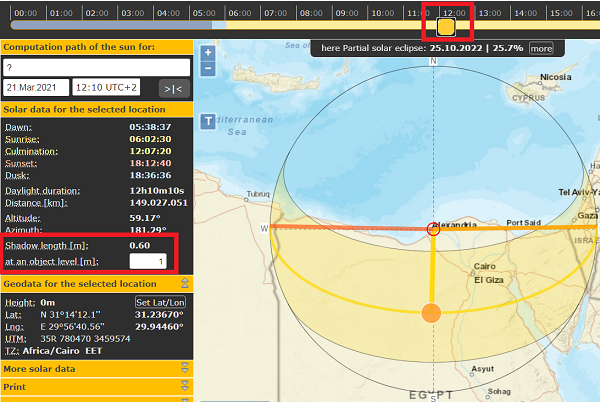
Syene (Aswan): Stick 1m. Shadow: 0.44 ..... alfa2: 23.75º

alfa1 - alfa2 = 30.96 - 23.75 = 7.2º
delta = 7.2º
Alexandria and Syene (Aswan) are not on the same longitude, therefore a miscalculation occurs, but it is small.
1 Like
7.- Proposal of app.
Look for a school that is in your same longitude, you get in touch with their teachers.
Make an application where the two schools can write the length of the shadow of a stick of 1 m on a certain day at a certain time.
Through CloudDB, the data of the other school will be obtained.
With these data (latitude, longitude, angles,...), calculate the radius of the Earth and the distance between schools.
1 Like
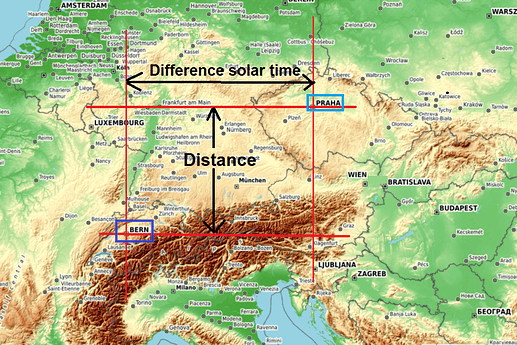
8.- Calculate the solar hour difference between two cities of the same latitude.
- Bratislava (48.151,17.136) and München (48.106,11.577), are in very similar latitude. Calculate the difference in solar time between those two cities.
- Create an application where you write the longitude of two cities and calculate the solar time difference and distance. (Watch out for Greenwich).
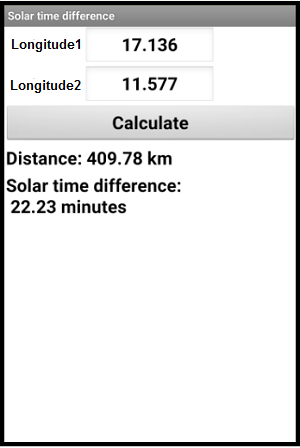
1 Like
9.- Create an application where you write the longitude and latitude of two cities and obtain the distance between their latitudes and the solar time difference.
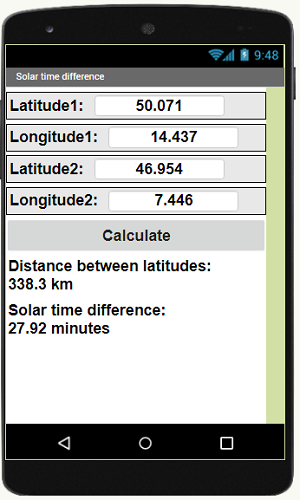
- In this way you can carry out the Eratosthenes experiment between two cities of different longitudes. Measure the shadow in Praha, 27.92 minutes later measure the shadow in Bern.
1 Like