How to determine the magnetic declination for virtually any place on the planet.
Magnetic declination is the difference between true North and magnetic North. The earth's magnetic field is constantly in motion.
Use the World Magnetic Model (WMM) World Magnetic Model (WMM) | National Centers for Environmental Information (NCEI)
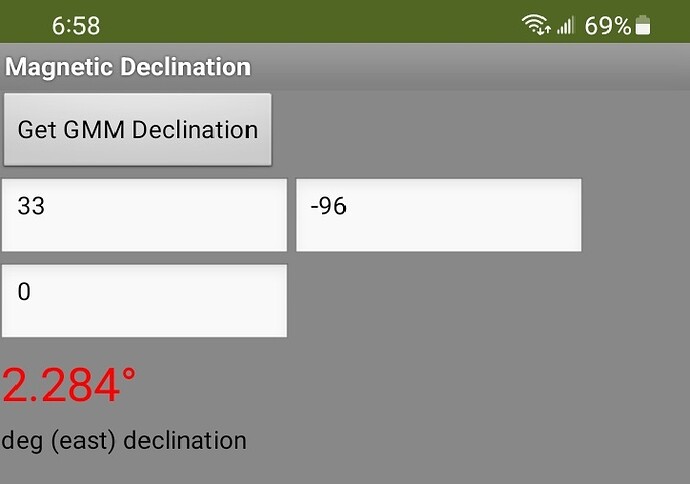
The app WMMdeclination provides the magnetic declination information available in your app through the use of the GMM model at World Magnetic Model Calculator
The app uses a GET request.
You can also get magnetic declination information for any latitude and longitude manually using the calculator at NCEI Geomagnetic Calculators
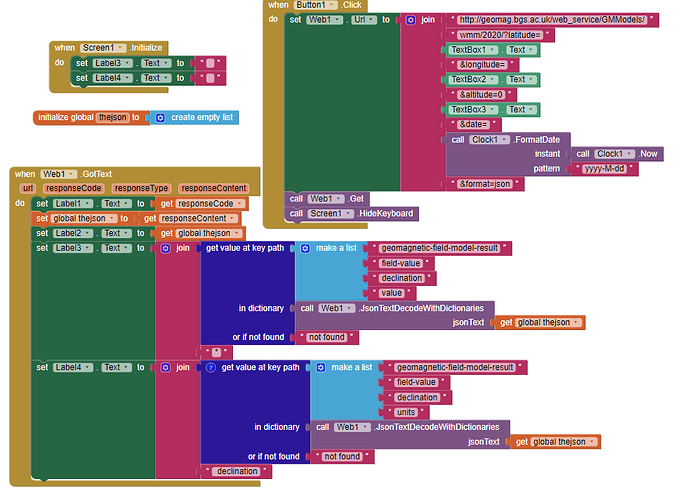
Magnetic declination can be calculated mathematically from the WMM algorithm or a Web page can do the calculation for you. Use a GET request at a site like World Magnetic Model Calculator to provide an xml or json file which will provide all the magnetic information. Once you have that file, use dictionaries or List blocks to extract what is needed.
The magnetic information for today's date can be read in xml or json format. Decode the file using a dictionary. The app uses json format. The declination value is provided in degrees ( ° ) and west or east of North . The declination is from the model; it is not an actual measurement of the declination.
Textbox1, Textbox2 and Textbox can be replaced by LocationSensor Latitude, Longitude and Altitude*0.001 (to provide the altitude in km; the LS provides this in meters) respectively. Using the dictionary you can also capture all the magnetic information used in WMM.
Latitude and Longitude should be in degrees. Altitude should be input in km. above MSL.
WMMdeclination2.aia (3.6 KB)
Regards,
Steve